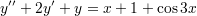MQN.gr

Νομίζω πως το μαθηματάκι μας απογοήτευσε κάπως,, τουλάχιστον εμένα και κάποιους φίλους μου... η παρακολούθηση κατά πόσο βοηθάει? κι ενας καλος βαθμός είναι δυνατός χωρίς αυτήν??

Αν έχεις Κραββαρίτη και προσέχεις τι λέει μπορείς να κρατήσεις πολύ καλές σημειώσεις που θα σου χρησιμεύσουν ως μπούσουλας στις εξετάσεις. Μην απογοητεύεσαι από τα μαθήματα της 1ης εβδομάδας, άλλωστε αυτό το εξάμηνο έχει πολύ πιο βαρετά μαθήματα και καθηγητές* . Αν δεν παρακολουθείς κανείς δεν σου εγγυάται ότι θα βρεις την φετινή ύλη ή σημειώσεις στην τελική.

*είναι ντόμινο, αν σταματήσεις να παρακολουθείς το ένα μάθημα, ακολουθούν και τα άλλα

Ιδού τι κάναμε στα 2 πρώτα μαθήματα (1ο τμήμα, κ.Κραββαρίτης):

7/10:
Συνήθεις Διαφορικές Εξισώσεις
Τάξη διαφορικής Εξίσωσης
Πρόβλημα αρχικών τιμών ή πρόβλημα Cauchy
Απλά παραδείγμτα επίλυσης διαφορικών εξισώσεων

8/10:
Διαφορικές εξισώσεις 1ης τάξης
1.Δ.Ε. χωριζόμενων μεταβλητών-Παραδείγματα
(Ορισμός ιδιαζουσών λύσεων)
2.Ομογενείς Δ.Ε. πρώτης τάξης

Επίσης να ενημερώσω ότι το μάθημα της Πέμπτης έγινε στα αμφιθέατρα του Κ.τηρίου Α.ντοχής Υλι.κών στα αμφιθέατρα 201 και 202 και όχι στο αμφιθέατρο Τεχνικών Υλικών όπως λέει το πρόγραμμα.

Χτες (14/10) κάναμε στο 1ο τμήμα:
Πολλαπλασιαστής Euler
Απειρία Πολ. Εuler
Υπολογισμός Πολ. Euler
Γραμμικές συνήθεις διαφορικές εξισώσεις 1ης τάξης (& ομογενείς)

Σήμερα 21/10 αρχίσαμε τις γραμμικές διαφορικές εξισώσεις δευτέρας τάξεως και συγκεκριμένα ασχοληθήκαμε με: συναρτήσεις Bessel και Legendre ως παραδείγματα, θεώρημα ύπαρξης-μοναδικότητας, το σύνολο των λύσεων της ομογενούς ως γραμ. χώρος, γραμμική ανεξαρτησία λύσεων-ορίζουσα Wronski, γενική λύση μη ομογενούς.

Ξέρει κανείς αν έχει αποφασιστεί από τους δύο καθηγητές να κάνει το ένα 2ωρο την Τετάρτη ο ένας και το άλλο 2ωρο την Πέμπτη ο άλλος;

akis έγραψε:Ξέρει κανείς αν έχει αποφασιστεί από τους δύο καθηγητές να κάνει το ένα 2ωρο την Τετάρτη ο ένας και το άλλο 2ωρο την Πέμπτη ο άλλος;

εμ αν καποιοι μιλάνε στο μαθημά πως να το ακουσουν!!!!!!!!!!!!!!!!!!!!

akis έγραψε:Ξέρει κανείς αν έχει αποφασιστεί από τους δύο καθηγητές να κάνει το ένα 2ωρο την Τετάρτη ο ένας και το άλλο 2ωρο την Πέμπτη ο άλλος;

Από τον κ. Κραββαρίτη ειπώθηκε σήμερα ότι από την επόμενη εβδομάδα τα δύο τμήματα θα κάνουν πάλι χωριστά, για όποιον ενδιαφέρεται.

22/10/09: Μιλήσαμε για τη λύση ομογενών γραμμικών διαφορικών εξισώσεων δευτέρας τάξης με τη μέθοδο υποβιβασμού τάξης, καθώς και για τις γραμμικές διαφορικές εξισώσεις δευτέρας τάξης με σταθερούς συντελεστές. Επίσης, ο κ. Κραββαρίτης μας έβαλε 2 ασκήσεις, τις οποίες όποιος θέλει μπορεί να φέρει στο επόμενο μάθημα:

29/10

Μετατροπή της λύσης της γραμμικής διαφορικής εξίσωσης δευτέρας τάξης σταθερών συντελεστών με Δ<0 σε μορφή χρήσιμη για τη φυσική (ημιτονοειδή συνάρτηση με πλάτος και αρχική φάση)
Μέθοδος μεταβολής των αυθαίρετων συντελεστών για εύρεση μιας μερικής λύσης της διαφορικής εξίσωσης και γενική λύση της μη ομογενούς
Παραδείγματα ομογενούς και μη ομογενών διαφορικών εξισώσεων

5/11

Μέθοδος Προσδιοριστέων Συντελεστών (3 περιπτώσεις)
Εύρεση μερικής λύσης δ.ε. ως άθροισμα δύο άλλων μερικών λύσεων

Επίσης, στο πρώτο τμήμα, ο καθηγητής μάς έβαλε να λύσουμε δύο ασκήσεις, τις οποίες μπορούμε να παραδώσουμε την επόμενη φορά:
Να λυθούν οι διαφορικές εξισώσεις:
1)
2)